Explanation of the S.M.Usherenko effect based on the shell model of the atom

This document has been translated and published with a voiceover by Bob Greenyer, with the permission of the principal author Alexander L. Shishkin and the article is speaking from his perspective having conducted more than 50 years of continual research in this specialist field.

---

1. Shell model of the atom

Theorists Dubovik V.M. and Kouroles V.K. state [1, 2]¹², that near atomic nuclei, dense vortex shells of prima-materia particles - background cold neutrinos (BCN) exist. According to the model of V.K. Kouroles each such shell consists of 0.771*10^11 elementary vortices; each elementary vortex contains 0.89*10^10 dipole LC elements where L is elementary inductance and C is elementary capacitance. By analogy with cosmogonic phenomena, let us imagine that the atomic nucleus is a mini "neutron" hole absorbing from the vacuum BCNs through a suction vortex. The nucleus extracts energy from the BCNs and ejects the spent particles through another vortex, which is then topologically looped into the suction vortex. Therefore, a vortex of condensed prima-materia is formed near the nucleus. The "long range" Coulomb field of the nucleus attracts the electron. But at a short distance from the nucleus, the electron begins to be affected by a repulsive "short-range" magnetic field, whose strength near the nucleus exceeds the Coulomb force by orders of magnitude.

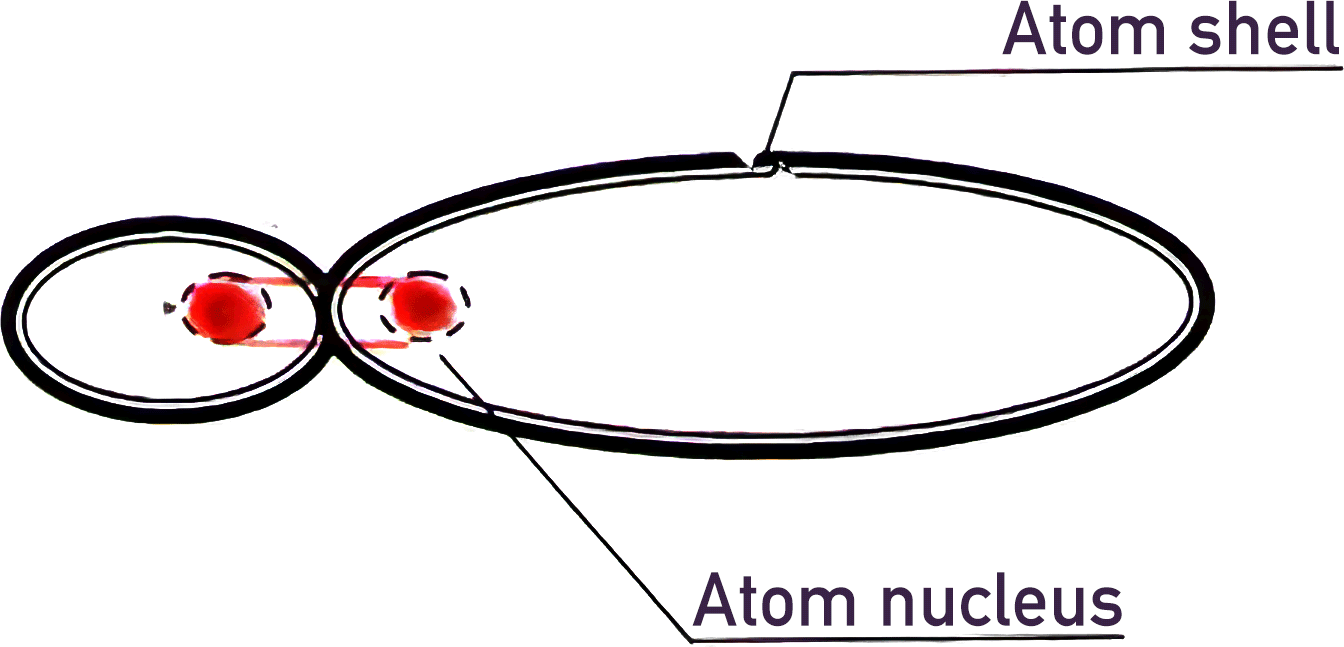
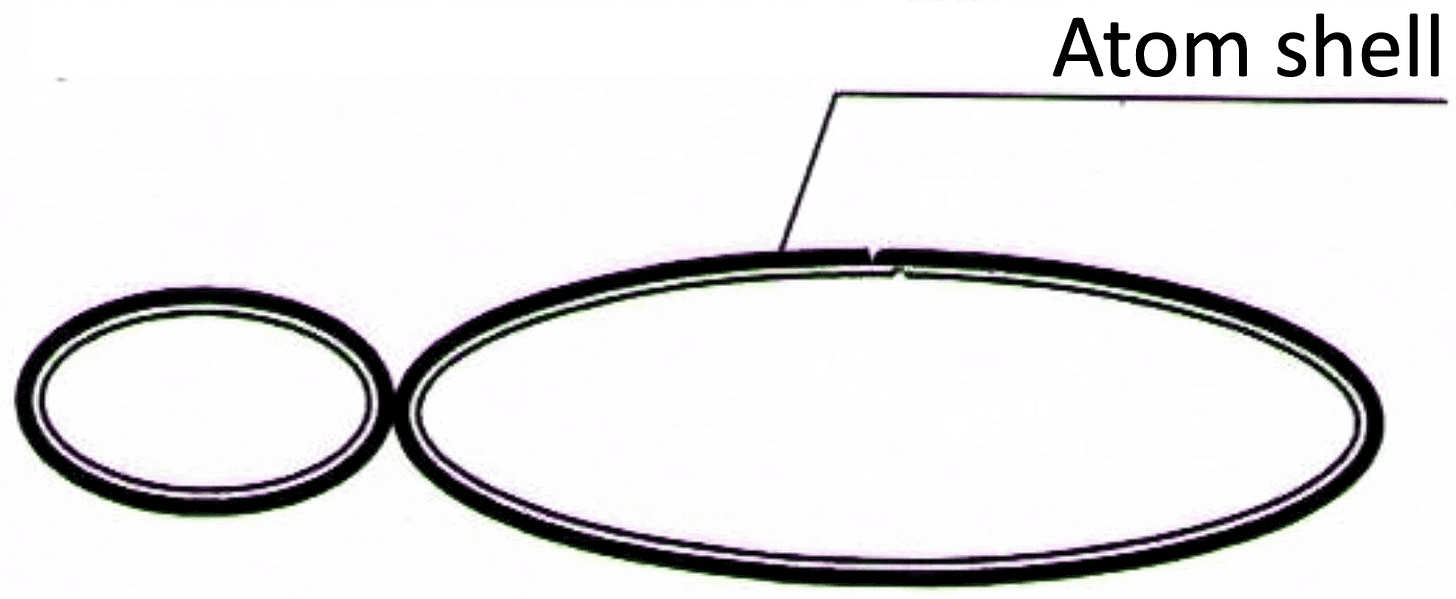
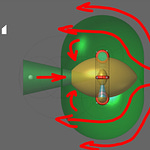
Therefore the electron, having received a portion of energy from the nucleus, flies away from it with even greater acceleration. When the speed of the electron increases above a certain critical value, the size of the electron changes in such a way, that the shell becomes impenetrable to it. Therefore the electron starts condensing the shell, pushing the BCNs away from the nucleus, towards its periphery. At the "Bohr" radius from the nucleus (3 to 30) * 10^-11 m, the electron loses energy, transferring it through the condensed shell of the atom to external BCNs. Here, it is slowed down by the outer shell and is again attracted by the Coulomb force to the nucleus. The process is repeated. Thus, the nucleus generates energy by absorbing vacuum BCNs, then it captures an electron, transfers a portion of energy to it, the electron in its turn transfers energy through the shell to the "vacuum" BCNs. According to V.K. Kuroles' model, the shell looks like an asymmetric "torus", with an extremely small central region, in the form of a nucleus (about 10^-15 m), which hangs on central vortices (Fig.1).

Thus, the atomic nucleus forms a toroidal vortex shell in the form of a soliton, with potential energy (Hartree energy) estimated at 0.394 * 10^17 eV = 0.631 * 10^-2 J. This condensed shell is extremely strong and elastic.

Fig.1. Simplified cross-section model of an atom.

The weakest point is the vortices on which the atom hangs. When there is a mechanical and/or electromagnetic impact on the atomic shell, a disturbance wave begins to tear one of the vortices away from the nucleus. According to various estimates, the critical impact energy is estimated to be between 5 eV and 10 eV. When the vortex detaches from the nucleus, the shell unpacks into a string (string-vortex soliton - SVS [2]), which flies away, turning in the opposite direction to the tear. After losing energy upon collision with matter, the "empty shell" rolls up into a torus-like vortex structure (vortex soliton) similar to the shell of an atom. The authors [1, 2] gave a name to this soliton, taking into account its properties - Magneto-Toro-Electric Cluster (MTEC). According to V.K. Kuroles' calculations, MTEC have the following characteristics:

1. An MTEC contains 6.93*10^20 elementary LC dipoles (background cold neutrinos (BCN) quanta).

2. An MTEC consists of 7.71*10^10 'electronic' vortices (EVs).

3. Each EV contains 0.89*10^10 elementary LC dipoles.

4. The mass (m) of an MTEC is about 1.0235*10^-40 kg.

5. Dynamic size of an MTEC:

   

   • length of the small torus ellipse - 0.52 µm,

   • length of the large torus ellipse - 15.5 µm,

   • diameter of the torus central part - 0.92 nm,

   • torus width - 0.5 µm,

   • torus thickness - 0.1 µm,

   • MTEC density (ρ) is about 1.30*10^-27 kg/cm³.

6. Under mechanical and/or other influences, an MTEC decays with the emission of 0.77*10^11 electrons accelerated to 10 keV and five orders of magnitude fewer ions, mostly protons, which agrees well with Ken Shoulders' experimental conclusions. Born matter has a mass of about 7.01*10^-20 kg.

2. An explanation of the Usherenko effect

The essence of the Usherenko effect [3, 4]³⁴ is that impactor particles of 10 to 100 microns in size, accelerated to a speed of the order of Vk = 1 km/s, pierced through a steel target 200mm thick, leaving a melted channel. A schematic of the setup is shown in Fig. 2. The energy released in the channel is hundreds of times greater than the kinetic energy expended on acceleration of such a particle. The channel penetrated by such a particle is filled with new chemical elements which are absent in the rest mass of the material. Experimenters [5]⁵ found that Usherenko effect is accompanied by electromagnetic and X-ray radiation.

All this indicates that the Usherenko effect involves a "cold" nuclear transformation of elements. And excess heat is the result of this transformation.

Fig.2. Apparatus for the processing of a metal target with microparticles. The device includes: an electrical detonator 1, an explosive cup 2, explosive charge 3, shaped deflector 4, micro-particle powder 5, guide cup 6, steel target-obstacle 8. Arrows show the flow of accelerated micro-particles 7 and the channels they produce 9 - there are traces of micro-particles in the thickness of steel target 8. Cup 2 has a capacity for up to 200 g of explosives. Ammonal (ammonium nitrate and aluminium powder) etc. is used as an explosive. Cups 2 and 6 are made of plastic.

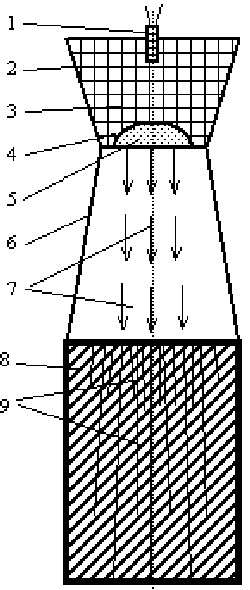
The device in Fig. 2. works as follows:-